티스토리 뷰
\(X\)와 \(Y\) set에 대해 함수 \(f : X \to Y\)가 bijection(일대일 대응)이라고 하자
책의 흐름 정도로만 정리하고 있기에 밑의 블로그 글에 엄밀한 설명이 나와 있으므로 참고한다.
https://aerospacekim.tistory.com/50
[선형변환부터 동형사상까지] ch8. 동형사상
이전 읽을거리 : [선형변환부터 동형사상까지] ch7. 가역인 선형변환 본 포스팅은 '프리드버그 선형대수학(5판)'을 공부하며 작성하였습니다. 11. 동형사상 ※ 본 포스팅의 도입부는 다소 엄밀하지
aerospacekim.tistory.com
동형사상(Isomorphic)에 대해 배워볼 것이다. 우선 Linear Operator에 관한 개념을 상기시키면서 알아보자.
\(X, Y\)을 임의의 set라고 하고, \(f : X \to Y\)을 함수라고 하자.
1. 모든 \(x_1, x_2 \in X\)에 대해 \(f(x_1) = f(x_2)\) 즉, \(x_1 = x_2\)을 만족하면 필요충분조건으로 \(f\)는 일대일함수이다. (Injective function)
2. 공역의 원소 \(y \in Y\)와 정의역의 원소 \(x \in X\)에 대해 공역의 원소가 그 원소를 함숫값으로 하는 정의역 원소가 최소한 하나라도 존재하면 \(f\)를 surjective한 함수라고 한다.
3. surjective 함수에서 최소한 하나가 아닌 오직 하나인 경우 bijective한, 일대일 대응 함수라고 한다.
vector space setting뿐만 아니라 어느 set이나 func에도 적용 가능한 개념이다. 고등학교 수학에서 다들 배워봤을 것이다. 이를 기반으로 역함수도 정의할 수 있다. 다음과 같다.
\(X\)와 \(Y\)를 set라 하고, \(f : X \to Y\)를 주어진 함수라고 하자. 만약 \(f^{-1} : Y \to X\), \(f\)의 역함수가 정의되면, \(f\)는 bijective하다. 즉, 함수 \(f\)가 일대일 대응이라는 것이다. 또한 다음을 만족한다.
\[f^{-1}(f(x)) = x\] for \quad all \quad \(x \in X\)
\[f(f^{-1}(y)) = y\] for \quad all \quad \(y \in Y\)
고등학교 수학 과정에서 다들 배웠을 것이다...증명 또한 선형대수학 관점에서도 비슷하게 흘러간다.
증명) \(f\)가 bijective, 일대일 대응이며, \(f^{-1} : Y \to X, f^{-1}(y) = x\)이라고 가정하자. \(f^{-1}\)이 well-defined 됐는지 확인해야 한다. \(f\)가 surjective하므로 모든 \(y \in Y\)에 대해 \(f(x) \ y\)를 만족하는 \(x \in X\)가 존재한다. \(f\)가 injective하므로 그런 x 또한 존재하므로 \(f^{-1}\)는 well-defined 됐다.
어느 \(x \in X\)에 대해 \(y = f(x)\)라고 하자. \(f^{-1}(y) = x\)이고, 이는 \(f^{-1}(f(x)) = x\)를 만족한다. 반대의 경우에도 \(y \in Y\), \(x = f^{-1}(y)\)에 대해 \(f(x) = y\)이며, \(f(f^{-1}(y)) = y\) 일대일 대응이므로 \(f(x_1) = f(x_2)\)인 \(x_1, x_2 \in X\)에 대해서도 위의 식을 만족하며 이는 \(x_1 = x_2\)를 함축한다. 이는 함수가 injective하다는 의미이다. \(Y\)의 원소, y에 대해서도 \(x = f^{-1}(y)\)인 식은 \(f(x) = f(f^{-1}(y)) = y\)를 만족하며 f는 surjective하다는 것을 알 수 있다. 그러므로 \(f^{-1}\)가 존재한다는 것은 bijective하다는 의미와 동치이다.
다음 이론은 함수와 그에 대한 역함수는 서로가 유일하다는 것이다.
\(X\)와 \(Y\) set에 대해 함수 \(f : X \to Y\)가 bijection(일대일 대응)이라고 하자. 이때 \(f^{-1}\)가 유일한 inverse function으로 존재한다. \(g = f^{-1}\)
\[g(f(x)) = x, for all x \in X \]
\[f(g(y)) = y, for all y \in Y \]
증명은 Exercise 2에서 하는 걸로 한다.
inverse function에 대해 다음과 같이 정리할 수 있다.
\(X\)와 \(Y\) set에 대해 \(f : X \to Y\)가 함수라고 가정하자. inverse function \(f^{-1}\)가 존재하면, \(f\)는 invertible하다.
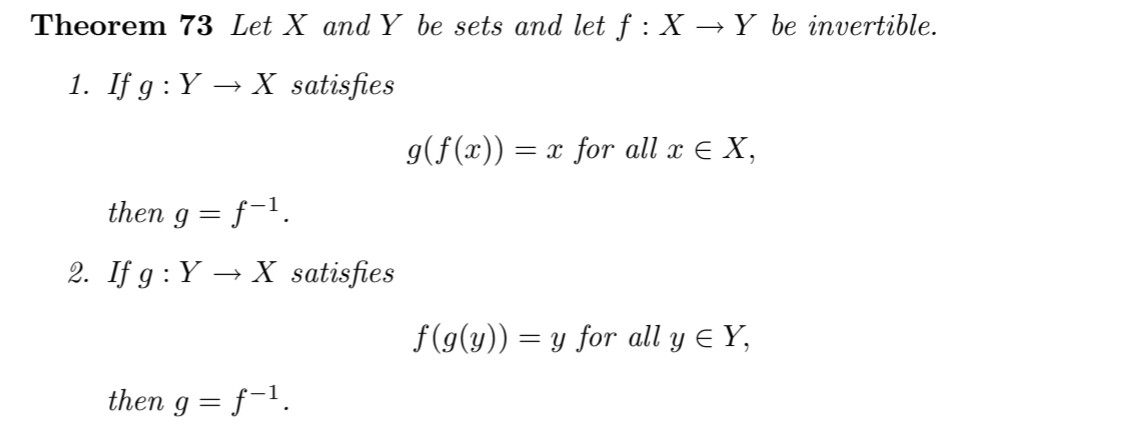
이렇게 같은 set이지만, 다르게 표현하고 있는 경우 두 set들을 Isomorphic이라고 한다. 자세한 정의는 다음과 같다.
\(X, Y\)를 finite-dimensional vector spaces라고 하자. \(E : X \to Y\)의 bijective linear operator가 존재하면, \(X\)와 \(Y\)를 isomorphic한 관계라고 하며, 명제의 역 또한 성립한다.
vector space가 세 개인 경우도 마찬가지이다. \(X, Y, X\)의 vector space에 대해 \(X\)와 \(Y\), \(Y\)와 \(Z\)가 각각 isomorphic 관계라고 하면, \(X\)와 \(Z\) 또한 isomorphic 관계이다.
증명) 연습문제 15
다음과 같은 이론도 성립한다.
\(X\)와 \(Y\)가 n차원 vector space라고 하면, \(X\)와 \(Y\)는 ismorphic 관계이다.
증명) \(x_1, x_2 \cdots x_n\), \(y_1, y_2 \cdots y_n\)을 각각 \(X\)와 \(Y\)의 basis라고 하자. \(E : X \to Y\)에 대해 \[ x = \alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n\] 인 x에 대해 \[ E(\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n) = \alpha_1 y_1 + \alpha_2 y_2 + \cdots + \alpha_n y_n\] 조건을 만족한다 하자. Operator E는 well-defined. E가 linear하다는 것은 연습문제 16에 있다는데, 이는 이미 앞 장에서 증명한 방식과 별 차이가 없을 것이다. 다음으로 E가 일대일대응임을 증명해야한다.
먼저 E가 surjective, 즉, 위로의 함수라고 해보자. \(x_1 = x_2\)이면 이에 대한 함숫값도 같아야 하는데, y를 \(Y\)의 임의의 원소라고 하면, 스칼라 \(\alpha\) set에 따라 \( y = \alpha_1 y_1 + \alpha_2 y_2 + \cdots + \alpha_n x_n\)이고, x 또한 이런 식으로 정의하면, operator E의 정의에 따라 \(E(x) =y\)가 성립한다. 즉, y 공역에 대해 대응하는 x 정의역이 존재하면서, E는 surjective하다.
다음으로 E가 injective, 일대일 함수라고 하자. \(u, v \in F\)에 대해 \(E(u) = E(v)\)가 만족한다고 하자. 또한, \( u = \alpha_1 x_1 + \alpha_2 x_2 +\cdots \alpha_n x_n \), \(v= \beta_1 x_1 + \beta_2 x_2 + \cdots \beta_n x_n\)을 만족하는 스칼라 집합 \(\alpha_1, \alpha_2, \cdots \alpha_n\), \(\beta_1, \beta_2 \cdots \beta_n\)이 존재한다. 이를 operator에 적용하면,
\[E(u) = E(v) \Rightarrow u = \alpha_1 y_1 + \alpha_2 y_2 +\cdots \alpha_n y_n = \beta_1 y_1 + \beta_2 y_2 + \cdots \beta_n y_n\]
즉 \( \alpha_1 = \beta_1, \alpha_2 = \beta_2, \cdots \alpha_n = \beta_n\)을 만족한다는 의미이다. 이는 u=v라는 의미를 함축하며 E가 injective하다는 것도 증명이 되며 E는 bijective한 operator이다.
동형사상에 관련된 기호들을 볼 것이다. 다음 사진 필기를 참고하자. 밑의 사진은 위의 블로그에서 발췌해온 것이다.

\( [x]_\chi = a\)의 정확한 의미는 다음 예시와 같이 이해하면 된다.



이런 동형사상을 그림으로 표현한 것은 다음 사진과 함께 설명을 이어가는 걸로 하겠다.

n차원 vector space \(X\), m차원 vector space \(U\)에 대해 \(E_X : X \to F^{n}\) Linear operator와 \(E_U : U \to F^{m}\) Linear operator에 대해 위의 식을 만족하며, 두 operator는 isomorphism 관계이다. 이를 감안해서 다음 사진과 같이 나타낼 수 있다.

\(A = E_U L E_X^{-1} (e_j) = E_U L(x_j)\)를 만족한다. 이는 이 식 의 notation으로 나타낼 수 있다.







블로그의 선형 변환에 관한 예시를 발췌해왔다. 선형대수학이 유용한 이유 중에 하나가 바로 미분이 단순 행렬 계산으로 빠르게 풀리며, 이를 다른 문제에서도 적용을 가능하다는 점을 깨달았다.


중요하다고 생각되는 문제를 가져왔다.
'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 3.5 - Existence and uniqueness off solutions (0) | 2023.11.13 |
|---|---|
| [선형대수학] Ch 3.4 - Linear Operator Equations (0) | 2023.10.16 |
| [선형대수학] Ch 3.2 - More Properties of Linear Operators (0) | 2023.10.16 |
| [선형대수학] Ch 3.1 - Linear Operators (0) | 2023.10.14 |
| [선형대수학] Ch 2.8 - Polynomial interpolation and the Lagrange basis (0) | 2023.10.14 |
