[선형대수학] Ch 4.3 - Practical computation of det(A)

앞선 Ch 4.1~4.2를 적용한 example을 하나 풀어보자. 열 및 행을 통째로 바꿀 때마다 부호가 바뀌는 것을 주로 적용한다.

여기서 upper triangle matrix를 만들면 determinant 값은 대각행렬을 전부 곱한 값인데, 이에 관한 이유는 뒤에서 얘기할 예정이다. 일단, 매우 중요하니 암기는 해두자.

---

A recursive formula for det(A)

이제 nxn matrix에서 n이 엄청 커도 determinant 계산하는 식에 대해 알아볼 것이다. 그 전에 알아둘 다음 이론을 한 번 보자.

pf)

이제 이를 이용한 determinant 공식이 나온다!! 매우 중요하니 자세히 보자!

pf)

이와 관련한 example 한 번 보겠다!

 

 

이로써 맨 첫 번재의 계산에 대한 의문성을 풀 수 있다!

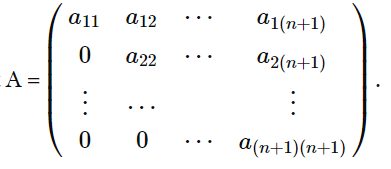
이런 upper triangle matrix에서

\(a_{11}\)에 대해 다음을 만족하고, 이를 계속 반복하면, 

이렇게 나오는 것이다.

---

Cramer's rule

이 공식은 연립 방정식의 해를 구하는 방법 중에 하나로, 다음과 같다.

뭔 소리인가 싶다.

이렇게 증명이 된다고 한다...하지만 와 닿지 않아서, 다른 방식으로 이해시켜보려고 한다.

출처 : https://blog.naver.com/PostView.naver?blogId=cj3024&logNo=221110397865

그렇다..\(x_n\)의 n열에 c 를 넣어서 계산한 determinant 나누기 detA가 \(x_n\)이다.