티스토리 뷰
선형대수학
[선형대수학] Ch 4.5 - Eigenvalue and the characteristic polynomial
hyuna_engineer 2023. 11. 27. 02:10
ch 4.4는 앞 절에서 얘기한 polynomial 얘기랑 같아서 생략한다.
이제 드디어 eigenvalue가 뭔지 얘기를 해보고자 한다.
일단 다음 영상이 도움이 되므로 한 번 가볍게 보고 오는 것이 좋을 것 같다.
https://www.youtube.com/watch?v=xDARfmKauuA
일단 영상의 내용을 좀 정리해보았다.
Eigenvalue란?
\[Av = \lambda v \]
위에서 \(\lambda\)는 eigenvalue, v는 eigenvector이다. \(\lambda\)는 Field에 속하는, 일종의 상수이다.
여기서 A는 mxn, v는 nx1 matrix이면, 우변이 나오기 위해서는 m=n이 되어야 하며, A는 정사각 행렬이다.
왜 eigenvalue가 중요한가?
이제 수식적으로 알아보자. 우선 \(det(\lambda I - A)\)의 계산은 다음과 같다.

pf)

이는 det(rI-A)는 일종의 다항식 형태가 되기에 다음과 같이 정의한다.

또한 A의 digonal element들에 대해 다음과 같이 정의한다.
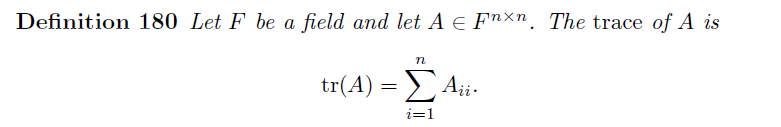
Example을 보자.


이제 eigenvalue를 구하는 데에서 그치지 말고, x의 값, eigenvectors도 구하는 것으로 한다. 다음 Example을 보자.


'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 4.7 - Eigenvalues of linear operators (0) | 2023.11.28 |
|---|---|
| [선형대수학] Ch 4.6 - diagonalization (0) | 2023.11.27 |
| [선형대수학] Ch 4.3 - Practical computation of det(A) (0) | 2023.11.27 |
| [선형대수학] Ch 4.2 - Further Properties of the determinant function (0) | 2023.11.26 |
| [선형대수학] Ch 4.1 - The Determinant Function (0) | 2023.11.26 |
