티스토리 뷰
우리가 흔히 알고 있는 (nonzero) vector x, y 에 대한 내적, <x,y>은 다음과 같다.
\[x \cdot y = ||x||_2||y||_2cos(\theta)\]
\(\theta\)는 x,y 사이의 angle이다. 여기서 \(\theta\)가 90도이면, 내적이 0인 것 또한 기하를 어느 정도 알고 있는 학생이면 잘 알 것이다. 즉, <x, y>=0일 때, 필요충분조건으로 다음을 만족한다.
\[||x+y||^{2} = ||x||^{2} + ||y||^{2}, \quad ||x-y||^{2} = ||x||^{2} + ||y||^{2}\]
\[||x+y||^{2} = <x+y, x+y> = <x, x> + 2<x,y> + <y, y> = ||x||^{2} + 2<x,y> + ||y||^{2} = ||x||^{2} + ||y||^{2}\]
x-y 일 때도 같다.
Orthogonal Bases

\(u_1, \cdots u_k\)가 V의 orthogoanl subset(V에 수직인 부분공간)일 때, 이 집합은 linearly independent하다는 것이다.
pf) \(c_1, c_2 \cdots c_k\)가 real number 집합이라고 하고, 다음을 만족한다고 하자. 저 집합이 linearly independent하다고를 고려해서 다음을 만족한다고 하자.
\[ c_1u_1 + c_2u_2 + \cdots + c_ku_k = 0\]
\(u_j\)과 내적하면,
\[<c_1u_1 + c_2u_2 + \cdots + c_ku_k, u_j> = <0, u_j> \]
\[\Rightarrow c_1<u_1, u_j>+ c_2<u_2, u_j> + \cdots +c_k<u_k, u_j> = 0 \cdots (1)\]
u vector 집합은 orthogonal subset 집합이므로 i \(\neq\) j 를 제외하고, 나머지 벡터끼리의 내적은 0이 된다. 즉, (1)은 다음과 같이 정리된다.
\[||u_j||^{2} c_j = 0\]
orthogonal set이므로 \(u_j\)은 nonzero vector이다. 그러므로 \(c_j\) = 0이어야 한다. j=0부터 k까지를 만족해야 하며, 벡터에 곱해지는 상수가 전부 0이 되는데, u 벡터 집합이 linearly independent하다는 이론은 증명됐다.
본격적으로 이 orthogonal basis 구하는 방법을 알아볼 것이다.

pf)
v와 \(u_j\)를 내적해보자. 6.13의 양변에 적용하면,
\[< v, u_j > = < \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n, u_j> \]
\[ = \alpha_1 <u_1, u_j> + \alpha_2 <u_2, u_j> + \cdots + \alpha_n <u_n, u_j> \]
i \(\neq\) j 를 제외하고, 나머지 벡터끼리의 내적은 0이 되므로(orthogonal basis 이기 때문) \(<v, u_j> = \alpha_j <u_j, u_j>\). 즉, 다음을 만족한다.
\[ \alpha_j = \frac{<v, u_j>}{<u_j, u_j>}\]
만약, basis들이 standard basis이면, \(\alpha\) 식에서 분모는 1이므로 \(\alpha_j = <v, u_j>\)로 간단하게 나타낼 수 있다.
예시를 보면서 더 이해를 높여보자.
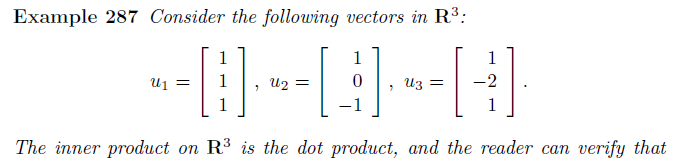
위의 u 벡터들은 \(R^{3}\)에서 orthogonal basis를 생성한다고 하자. \(v = (1,3, -1)\)과 내적을 해보자.

Dot product 말고 polynomial product일 때도 보자.
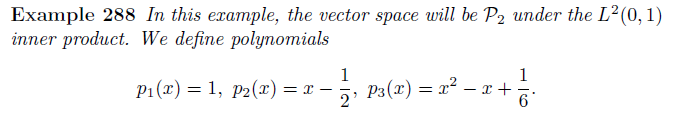
위의 조건에서 \(q(x) = x^{2} + 2x + 3\)인 것을 고려해서 q(x)와 P를 내적한 것을 구해보자.
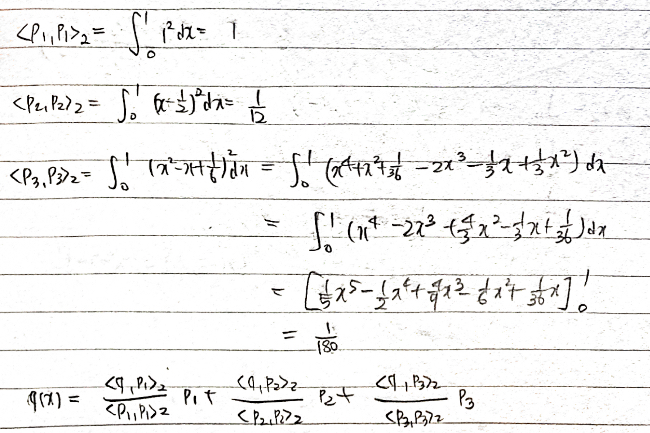

'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 6.5 - The Gram-Schmidt process (0) | 2023.12.01 |
|---|---|
| [선형대수학] Ch 6.4 - The Projection Theorem (0) | 2023.11.30 |
| [선형대수학] Ch 6.2 - The adjoint(수반연산자) of a linear operator (0) | 2023.11.30 |
| [선형대수학] Ch 6.1 - Norms and inner products (0) | 2023.11.28 |
| [선형대수학] Ch 4.7 - Eigenvalues of linear operators (0) | 2023.11.28 |
