[선형대수학] Ch 6.1 - Norms and inner products

 우리는 Ax = b 계산할 때, free variable에 대해 basis가 span한 공간의 특성만 나타내고 정확한 해를 구하지는 못했다. 이를 해결하기 위한 것이 이번 장이다. Ax = b를 근사하게 만족하는 근사 해 x를 구하는 방향으로 x를 구할 것이다. 근사 해 구할 때 projection으로 해를 구하는 것이다. 그 전에 벡터의 크기를 무엇인지 알아야 한다.

---

1. 크기는 항상 양수이다.

2. 실수 곱은 크기 구할 때 분리 법칙 적용 가능

3. 두 벡터를 더한 것의 크기는 항상 각각의 크기를 더한 것보다 작다. 3.은 삼각형 변 길이를 추측할 때 쓰이던 방법이다. (제 기억으로는 아마 초등학교 때 했던 걸로..)

밑의 사진을 보면 3.은 더 잘 이해될 것이다.

크기를 구하는 방법은 다음과 같다.

위의 크기를 구하는 방법을 Euclidean Norm 이라고 불린다.

 

내적을 구하는 방법은 다음과 같다.

점 내적과 관련된 벡터 내적이며, 사실 여기까지는 기하에서 다 배운 내용일 것이다. 앞으로 이 점 내적이 항상 맞는 것은 아닐 것이기에 복습하는 느낌으로 내적의 공식은 이랬지 하고 넘어간다.

 

내적을 표시하는 방법이 있다. 바로 <x, y>으로 표시한다. 이와 관련하여 성질도 다음과 같다.

6.2 성질과 w에 alpha, beta가 붙을 때의 분리 법칙 또한 가능하면, <u,w>를 bilinear하다고 한다. 

pf)

 

 

Norm과 관련된 부등식 이론은 다음과 같다.

pf)

u, v가 zero vector일 때는 자명한 사실. 

u, v가 nonzero vector일 때를 보자. <u, u> = <v, v>=1 인 경우를 살펴보자. 6.3에 의해 <u-v, u-v> $\ge$ 0을 만족한다. 여기에 6.2 성질을 적용하면, 

$$<u-v,u-v>=<u,u>-2<u,v>+<v,v>=2-2<u,v>$$

$$2-2<u,v>\ge 0\Rightarrow <u,v>\le 1$$

위의 증명으로 <u+v, u+v> $\ge$ 0을 만족하면서 이는 $-1\le <u,v>$ 로 도출되면서, $|<u,v>|\le 1$을 만족함을 알 수 있다. 

 

이제 general한 case를 보자면, u,v가 nonzero vector이고, $u,v\in V$일 때, $\hat{u}$과 $\hat{v}$을 다음과 같이 정의해보자.

$$\hat{u}=<u,u{>}^{-1/2}u,\hat{v}=<v,v{>}^{-1/2}v$$

이때, u hat의 크기는 

1을 만족하면서, v hat에 대해서도 했을 때도 1이 나온다. 이는  $|<\hat{u},\hat{v}>|\le 1$ 을 만족한다. 이는, 

을 만족하면서, 최종적으로

을 만족하면서 이론을 증명했다. 

 

이제 이를 이용해서 벡터의 내적(inner product)을 구하도록 해보자.

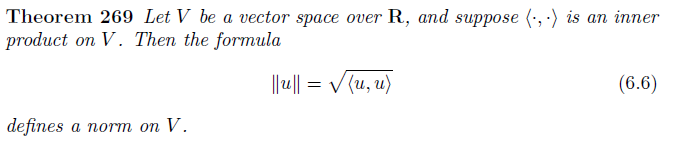
pf)

definition 265의 1~3을 다 만족하는지 확인하면 된다.

1) 3)을 증명하면서 같이 증명 가능하다.

2) $\alpha \in R$과 어느 $v\in V$에 대해 다음을 만족한다.

$$||\alpha u||=\sqrt{<\alpha u,\alpha u>}=\sqrt{{\alpha }^2}\sqrt{<u,u>}=\left|\alpha \right|||u||$$

3) triangle inequality로, Cauchy-Schwarz inequality를 이용하면 다음과 같다.

$$||u+v|{|}^2=<u+v,u+v>=<u,u>+2<u,v>+<v,v>=||u|{|}^2+2<u,v>+||v|{|}^2$$

$$\le ||u|{|}^2+2||u||||v||+||v|{|}^2=(||u||+||v||{)}^2$$

||u+v|| $\le$ ||u|| + ||v|| 를 만족한다.

 

---

이제 Norms와 inner product를 이용한 summation을 더 볼 것이다.

보통 점 곱은 다음과 같이 정의된다.

$$x\cdot y=\sum _{i=1}^n{x}_i{y}_{i}forallx,y\in R^n$$

이 점 곱은 Euclidean inner product라고 한다. 이에 관한 Euclidean norm은 다음과 같다.

$$||x|{|}_2=\sqrt{\sum _{i=1}^n{x}_i^2}forallx\in R^n$$

이를 일반화하면 다음과 같으며, $l^p$  norm라고 불린다.

$$||x|{|}_p=[\sum _{i=1}^n{\left|x_i\right|}^p{]}^{1/p}forallx\in R^n$$