티스토리 뷰
Transpose를 이용한 inner product와 이를 확장해서 linear operator일 때도 볼 것이다.
\[\sum_{j=1}^{n} \sum_{i=1}^{m} A_{ij}x_jy_i = \sum_{j=1}^{n} (\sum_{i=1}^{m} A_{ij}y_i) x_j = \sum_{j=1}^{n}(A^{T} y)_j x_j = x \cdot (A^{T} y) \]
위의 증명을 통해 다음 이론이 만족함을 알 수 있다.


The adjoint of a linear operator
Euclidean dot product를 이용해 Linear operator를 나타내면,
여기서 unique operator S를 adjoint of T라고 부른다.
이때까지는 점 곱(dot product)만 나타냈다면, 이 점 곱 내적을 행렬로 나타낸 것을 Gram Matrix라고 한다.

Gram matrix는 내적(inner product)의 특성을 행렬로 나타낸 것으로, 행렬의 열 벡터들 간의 내적으로 이루어진 정방 행렬입니다.
Gram matrix는 nonsingular matrix, 즉, determinant가 0이 아닌데, 그와 관련된 이론은 다음과 같다.

pf)

6.1에서 적용하던 성질을 Linear operator에 적용해볼 것이다.

이것은 Linear operator와 중요한 이론으로 교과서의 사진을 증명으로 제시하겠다.


설명을 하자면,

연습문제

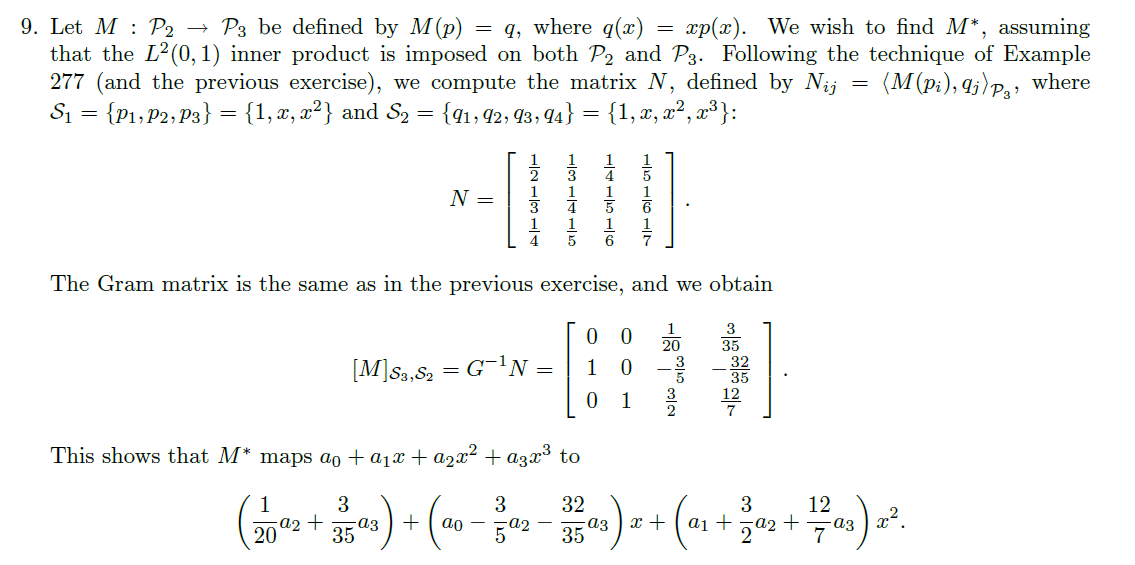
'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 6.4 - The Projection Theorem (0) | 2023.11.30 |
|---|---|
| [선형대수학] Ch 6.3 - Orthogonal vectors and bases (0) | 2023.11.30 |
| [선형대수학] Ch 6.1 - Norms and inner products (0) | 2023.11.28 |
| [선형대수학] Ch 4.7 - Eigenvalues of linear operators (0) | 2023.11.28 |
| [선형대수학] Ch 4.6 - diagonalization (0) | 2023.11.27 |
