티스토리 뷰
이전까지는 vector space를 basis로 쪼갰다면, 이제는 vector space를 subspace들로 쪼개보겠다. 이와 관련된 정의는 다음과 같다.

여기서 V가 내적 공간이고, S가 nonempty subset이면, S-perp 또한, zero vector 포함, addition, scalar mutliplication이 가능하면서 V의 subspace가 된다.
이와 관련된 예시를 보자.
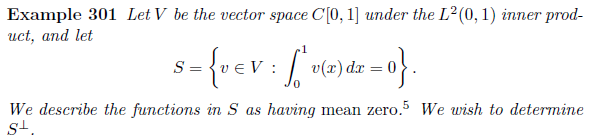

Orthogonal한 subspace 사이들의 특징을 알아보자.
1. S & T가 V의 orthogoanal subspace이면 \(S \cap T = {0} \)이다.
2. (\(S^{⊥}\))\(^{⊥}=S\)
3. S, T 모두 V의 subspace이면, S+V 또한 subspace라는 사실은 이전 챕터들에서 증명했다. S와 T가 orthogonal subspace들일 때는 S와 T의 direct sum으로 S⊕T 기호를 쓴다.
4. S, T가 V의 orthogonal subspace이면, \(dim(V) = dim(S) + dim(T)\)을 만족한다.
5. \(V = S ⊕ S^{⊥}\)을 만족한다.
3. 증명

5. 증명
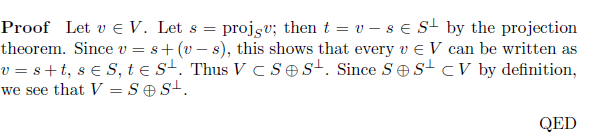
Fundamental Theorem을 이용하면, T*을 T:X -> U의 linear operator perp이라고 하자. 다음 성질을 만족한다. 증명도 같이 제시했다. rank(T) + nullity(T) = dim(X)임을 잊지 말자.

Fundamental Theorem과 관련해 여러 성질을 제시하고 끝 마치겠다.

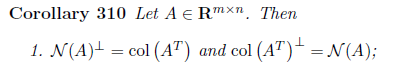
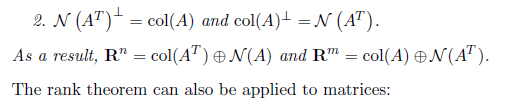


.
'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 6.7 - Complex inner product spaces (0) | 2023.12.01 |
|---|---|
| [선형대수학] Ch 6.5 - The Gram-Schmidt process (0) | 2023.12.01 |
| [선형대수학] Ch 6.4 - The Projection Theorem (0) | 2023.11.30 |
| [선형대수학] Ch 6.3 - Orthogonal vectors and bases (0) | 2023.11.30 |
| [선형대수학] Ch 6.2 - The adjoint(수반연산자) of a linear operator (0) | 2023.11.30 |
