티스토리 뷰
Fourier series는 유한한 정의역을 가진 주기 함수 안에서 수식으로 나타내기에 좋은 식이다.
하지만 우리가 접하는 함수는 비주기 함수인 경우가 대부분이다. 이번 장은 비주기 함수일 때 나타낼 수 있는 Fourier Integral를 배울 것이다. 주기가 없다는 것은 주기가 2L일 때의 L을 무한대로 보내면, 이것 또한 주기가 없다라고 할 수 있다. 이런 점을 이용해 식을 세워볼 것이다. 그 전에 Example로 잠시 확인해보자.

이렇게 L이 증가할수록 amplitude가 낮아지고, n의 간격이 넓어진다. 직관적으로 이해하면 좋을 것 같다. 다음은 수식 측면에서 알아보자.
Fourier series -> Fourier Integral로 전환하는 과정이다.
\[ f_L(x) = a_0 + \sum_{n=1}^{\infty} (a_n cosw_nx + b_nsinw_nx), w_n = \frac{n\pi}{L} \] 에서 L->\( \infty \)로 보내고자 한다. \(a_0, a_n, b_n \)에 Euler Formulas 공식들을 대입하자.
\[ f_L(x) = \frac{1}{2L} \int_{-L}^{L}f_L(v)dv + \frac{1}{L} \sum_{n=1}^{\infty} [cosw_nx\int_{-L}^{L}f_L(v)cosw_nvdv + \\ sinw_nx\int_{-L}^{L}f_L(v)sinw_nvdv] \]
\( \Delta w = w_{n+1} - w_n = \frac{(n+1)\pi} {L} -\frac{n\pi}{L} = \frac {\pi}{L} \) 라고 가정하면, \( \frac{1}{L} = \frac{\Delta w}{\pi} \)이므로,
\[ f_L(x) = \frac{1}{2L} \int_{-L}^{L}f_L(v)dv + \frac{1}{\pi} \sum_{n=1}^{\infty} [(cosw_nx) \Delta w \int_{-L}^{L}f_L(v)cosw_nvdv \\+ (sinw_nx) \Delta w \int_{-L}^{L}f_L(v)sinw_nvdv] \]
비주기 함수 ( nonperiodic function)가 다음을 만족하며 x축에서 absolutely integrable 하다고 하자. 절대적으로 적분가능하다는 말은 \(-\infty\)에서 \(+\infty\)까지 함수 절댓값을 적분했을 때 그 값이 발산하지 않는 것을 의미한다.
\[f(x) = \displaystyle \lim_{L \to \infty} f_L(x) \]
다음 limt 들은 존재한다.
\begin{align*}
\int_{-\infty}^{\infty}|f(x)|dx &= \lim_{{a \to -\infty}} \int_{a}^{0}|f(x)|dx + \lim_{{b \to \infty}} \int_{0}^{b}|f(x)|dx
\end{align*}
L이 무한대로 가면서 1/L은 0으로 수렴하고, Fourier series에서의 \(a_0\)=0이 된다. 또한 \( \Delta w = \frac{\pi}{L} \) 0으로 수렴하면서 \( \Delta w \)는 무시해도 될 수준이 된다. 즉, \(a_0, \Delta w \)가 없어지고,
\begin{align*}
f(x) = \frac{1}{\pi} \int_{0}^{\infty}[coswx \int_{-\infty}^{\infty}f(v)coswvdv + sinwx \int_{-\infty}^{\infty}f(v)sinwvdv]dw
\end{align*}
Notations들은
\[ A(w) = \frac {1}{\pi} \int_{-\infty}^{\infty} f(v)coswvdv, B(w) = \frac {1}{\pi} \int_{-\infty}^{\infty} f(v)sinwvdv \]가 된다.
최종적으로 f(x)는
\begin{align*}
f(x) = \int_{0}^{\infty}[A(w) coswx +B(w) sinwx ]dw
\end{align*}
가 되며, 이를 Fourier Integral라고 한다.

위의 사진은 Fourier Integral를 Theorem 1에 정리한 것이다. Example을 통해 적용을 알아보자.

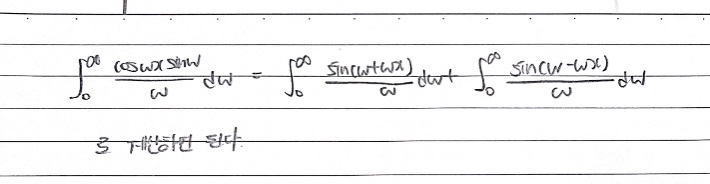
Fourier Cosine Integral과 Fourier Sine Integral에 대해 알아보자.
그 전 장에서 f(x)가 even, odd인지에 따라 fourier series가 간단해지는 것을 알았다. 이를 Fourier Integral도 같이 적용 가능하다. 만약 f(x)가 Fourier Integral을 가지고 even이면, B(w)=0이고, odd이면 A(w)=0이다.
i) f(x) = even function
\[ f(x) = \int_{0}^{\infty} A(w)coswxdw, A(w) = \frac{2}{\pi} \int_{0}^{\infty} f(v)coswvdv \]
ii) f(x) = odd funciton
\[ f(x) = \int_{0}^{\infty} B(w)sinwxdw, B(w) = \frac{2}{\pi} \int_{0}^{\infty} f(v)sinwvdv \]
Example로 알아보자. Laplace Integral에 관한 예제이다.



위에 나오는 두 식을 Laplace Integrals이라고 한다.
'Engineering Mathematics' 카테고리의 다른 글
| 12.1 Basic Concepts of PDEs (0) | 2023.10.11 |
|---|---|
| 11.9 Fourier Transform. Discrete and Fast Fourier Transforms. (0) | 2023.10.07 |
| 11.5 Orthogonal Functions & 11.6 Orthogonal Series. Generalized Fourier Series (1) | 2023.10.05 |
| 11.2 Arbitrary Period. Even and Odd Functions. Half-Range Expansions (0) | 2023.10.04 |
| 11. 1 Fourier Series (0) | 2023.10.02 |
