티스토리 뷰
11.9 Fourier Transform. Discrete and Fast Fourier Transforms.
hyuna_engineer 2023. 10. 7. 16:29
Fourier Transform을 알아볼 것이다. 왜 Fourier Transform을 배우냐하면, 시간 t 축에서의 신호, 정보를 주파수 w 축으로 옮겨오기 위해서 배운다. 주파수 축에서의 분석을 위한 수학적 계산들을 배울 것이다. 많은 공학 분야에서 쓰이고, 주로 신호 처리 분야에서 쓰인다.
Complex Form of Fourier Integral
11.7 장에서 Fourier Integral을 다음과 같이 배웠다.
\[ f(x) = \int_{0}^{\infty} [A(w)coswx + B(w)sinwx]dw \]
\[ A(w) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(v)coswvdv, B(w) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(v)sinwvdv \]
A(w)와 B(w)을 식에 대입하면,
\[ f(x) = \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} f(v)[coswvcoswx + sinwvsinwx]dvdw \]
삼각함수의 덧셈정리를 이용하면,
\[ f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} [\int_{-\infty}^{\infty} f(v)cos(wx-wv)dv]dw \]
에서 cos 대신 sin일 때는 0이다. 왜냐하면 dw에 대해 적분하면 x-v는 상수 취급되기에 sin(x-v)w는 기함수가 되기 때문이다.
Euler Formula(오일러 공식)를 \(e^{ix} = cosx + isinx\)을 이용해서 주파수 도메인에서 연산 및 분석을 간단하게 해보자. 오일러 공식의 증명은 밑에서 번외로 증명하겠다.
\[f(v)cos(wx-wv) + if(v)sin(wx-wv) = f(v)e^{i(wx-wv)} \]
Complex Fourier Integral은
\[f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(v)e^{iw(x-v)}dvdw \]
여기서 \(\frac{1}{2\pi}\)을 \(\frac{1}{\sqrt2\pi}\) 2개로 분리하면
\[ f(x) = \frac{1}{\sqrt {2\pi}} \int_{-\infty}^{\infty} [ \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(v) e^{-iwv}dv]e^{iwx}dw \]
여기서 []안에 있는 것을 Fourier Transform이라고 하며 정리하면,
\[ \hat{f(w)} = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}f(x)e^{-iwx}dx \]
이에 대한 역인 inverse Fourier Transform은
\[ f(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \hat{f}(w) e^{iwx} \, dw \]
Fourier Transform을 간략하게
\( \hat{f}\) = ℱ(\(f\)), \(f = ℱ^{-1}(\hat{f})\) 라고 한다. Inverse Fourier Transform의 존재성 관련 Theorem은 다음과 같다.
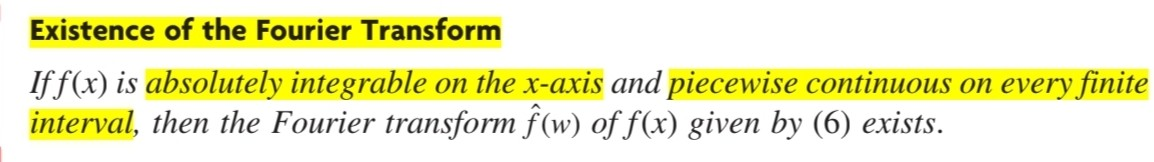
f(x)가 x축에 대해 절대적으로 적분 가능하고, 모든 유한한 구간에서 piecewise 연속하다면 Fourier Transform의 역이 존재한다. Example로 어떻게 쓰이는지 볼 것이다.

Fourier Transform의 특징에 대해 더 알아보자.
선형결합이 가능하다.

x가 무한으로 갈 때 f(x)가 0으로 수렴한다면 f(x)의 미분 형태인 f'(x)가 Fourier Transform에 들어가면 다음과 같다.


Fourier Transform의 중요한 개념인 Convolution에 대해 알아보자.
함수 f와 g의 convolution한 것을 h라고 했을 때,
\[ h(x) = (f \ast g) (x) = \int_{-\infty}^{\infty} f(p)g(x-p)dp = \int_{-\infty}^{\infty}f(x-p)g(p)dp \]

위의 성질도 만족한다. 증명은 다음 사진을 참고한다.

'Engineering Mathematics' 카테고리의 다른 글
| 12.3 Solution by Separating Variables. Use of Fourier Series (0) | 2023.10.12 |
|---|---|
| 12.1 Basic Concepts of PDEs (0) | 2023.10.11 |
| 11.7 Fourier Integral (1) | 2023.10.05 |
| 11.5 Orthogonal Functions & 11.6 Orthogonal Series. Generalized Fourier Series (1) | 2023.10.05 |
| 11.2 Arbitrary Period. Even and Odd Functions. Half-Range Expansions (0) | 2023.10.04 |
