티스토리 뷰
Linearly Independence에 대해 배울 것이다. 선형대수학에서 중요한 개념 중 하나이다.
그 전에 subspace에 대해 좀 더 알아보자. 앞으로의 설명에서 V is vector space over F라고 가정한다.
- 모든 \(V\)는 Subset을 갖는다.
- \(V\)의 가장 작은 spanning set을 B라 하면, \(V = span(B)\)이다.
2.와 관련된 보조 정리는 다음과 같다.
\(u_1, u_2, \cdots u_n \)dl \(V\)의 vectors이고, \(v \in sp{u_1, u_2, \cdots u_n} \)이면,
\(sp{u_1, u_2, \cdots u_n, v} = sp{u_1, u_2, \cdots u_n}\) 이다.
Proof) x를 \( sp{u_1, u_2, \cdots u_n} \)에 속하는 임의의 vector라고 하면, x를 \(u_1, u_2, \cdots u_n\)들의 선형 결합으로 나타낼 수 있다.
\[ x = \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n \]
이고, 이는
\[x = \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n + 0v\]
로 쓸 수 있다. 이는 x 또한 \(sp{u_1, u_2, \cdots u_n, v}\) 에 속한다고 할 수 있다. 즉,
\[x = \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n + \alpha_{n+1}v \]
v 또한 \(sp{u_1, u_2, \cdots u_n \)에 속한다고 할 수 있으며,
\[v = \beta_1 u_1 + \beta_2 u_2 + \cdots + \beta_n u_n\] 이며,
\[
x = \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n + \alpha_{n+1}v \\
= \alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n + \alpha_{n+1}(\beta_1 u_1 + \beta_2 u_2 + \cdots + \beta_n u_n) \\
= (\alpha_1 + \alpha_{n+1}\beta_1)u_1 + (\alpha_2 + \alpha_{n+1}\beta_2)u_2 + \cdots + (\alpha_n + \alpha_{n+1}\beta_n)u_n
\]
이는 x가 \(u_1, u_2, \cdots u_n\)의 선형 결합이며 x는 \(sp{u_1, u_2, \cdots u_n}\)에 속한다.
이제 본격적으로 Linear independence에 대해 알아볼 것이다. 정의는 다음과 같다.
\(u_1, u_2 \cdots u_n\)을 \(V\)의 vectors라고 하면, 만약, scalar \(\alpha_1, \alpha_2 \cdots \alpha_n\)에 대해 \(\alpha_1 u_1 + \alpha_2 u_2 + \cdots + \alpha_n u_n = 0\)을 만족하는 scalar들이 \(\alpha_1 = \alpha_2 = \cdots = \alpha_n = 0\)밖에 없다면 \(u_1, u_2 \cdots u_n\)은 Linearly Independent하다.
Scalar가 모두 0이어야 한다.
Example로 파악해보자.



선형 결합과 Linearly independence가 연관된 이론은 다음과 같다.
\(V\)에 대해 \(u_1, u_2, \cdots u_n\)이 \(V\)의 vectors라고 하고, \(n \geq 2\)라고 하자. 만약 이들 중에 하나의 벡터가 나머 벡터들의 선형 결합(Linear Combination)으로 나타낼 수 있으면 \(u_1, u_2, \cdots u_n\)은 Linearly dependent하다.
이에 대한 증명은 교재를 참고한다.

이는 \(u_i\)는 \(u_1, \cdots u_{i-1}, u_{i+1}, \cdots u_n\)의 선형 합으로 나타낼 수 있다는 의미이다. (전제 : scalar는 0이 아님.)

위의 증명은 하나의 벡터가 다른 벡터들의 선형 결합으로 이루어지지 않아야지 그 집합은 Linearly independent하다는 것이다. 이 이론에 관한 Example을 보겠다.

이번에는 span과 관련된 Linearly independence 이론이다.
\(V\)에 대해 \(u_1, u_2, \cdots u_n\)이 \(V\)의 vectors라고 하자. 만약, \(sp{u_1, u_2, \cdots u_n}\)의 각 벡터들이 \(u_1, u_2 \cdots u_n\)들의 선형 결합으로 유일하게 써진다면, 이 \({u_1, u_2, \cdots u_n}\)은 Linearly independent하다.
이에 대한 증명도 교재를 참고한다.
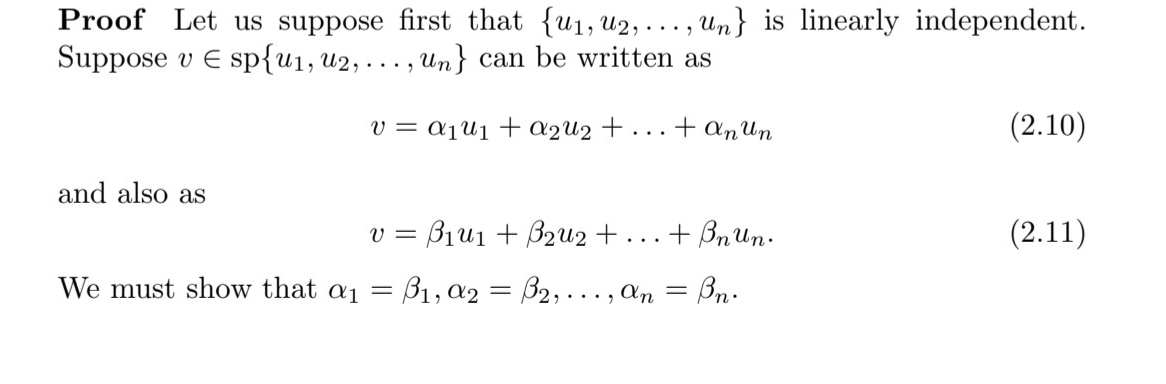

24와 26 이론은 언뜻 보면 같은 것 같다. 왜냐하면 둘 다 하나의 벡터가 나머지 벡터의 선형 결합 조합으로 된다면 24일 때는 dependent, 26일 때는 independent인데 왜 일까..그 이유는 26 이론에서 "unique", "유일하게“가 중요한 부분이다. 24의 예시처럼 \(\alpha_1=-3\alpha_3, \alpha_2=\alpha_3\) 꼴로 \(\alpha_1, \alpha_2, \alpha_3\)이 하나로 정해지지 않고 여러 경우가 존재하는 경우 dependent하다는 의미이고, 26은 \(\alpha_1 u_1+ \alpha_2 u_2+ ... +\alpha_n u_n=0 \)을 만들었을 때 \(\alpha_1=a, \alpha_2=b, \alpha_3=c \)로 하나로 “유일하게” 정해지면 linearly independent하다는 의미인 것이다.
'선형대수학' 카테고리의 다른 글
| [선형대수학] Ch 2.7-Properties of bases(+3.7) (0) | 2023.10.14 |
|---|---|
| [선형대수학] Ch 2.6 - Basis and dimension (0) | 2023.10.13 |
| [선형대수학] Ch 2.4 - Linear Combinations (0) | 2023.10.12 |
| [선형대수학] Ch2.3 - Subspaces (0) | 2023.10.12 |
| [선형대수학] Ch2.2 - Vector Spaces (0) | 2023.10.11 |
