13.3 Derivative. Analytic Function

앞으로의 내용 설명에 앞서 개념들을 설명해보겠다.

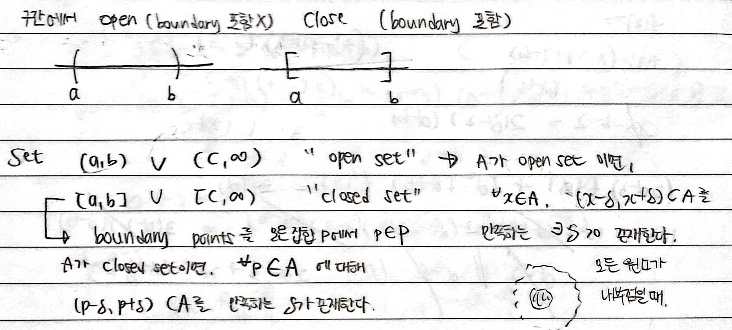
 open set과 closed set에 관한 정의 및 차이는 boundary point를 기준으로 나뉘는 것이다. 또한, open set 여러 개에 대해 disconnected 되어 있다는 의미는 말 그대로 교집합이 없다는 의미이고, open set이어도 접하는 점이 하나라도 존재하면 이는 connected 되어 있다라고 얘기한다. 또한 추가적으로 어떤 점의 근방(neighborhood)란, 그 점으로부터 특정 거리 미만인 모든 점의 집합이다.  이후 14장에서 더 자세히 배울 예정이니 이 정도까지 하는 걸로 하자.

 

w = complex number라고 하고, w=u+iv라고 하자. u는 실수 부분, v는 허수 부분이다. w를 f라는 complex 에서 complex로 가는 함수의 y 값이라고 하자. 이에 대한 x값은 z(z;complex number)라고 하며 다음과 같이 나타낼 수 있다.

$$w=f(z)=u(x,y)+iv(x,y)$$ 

---

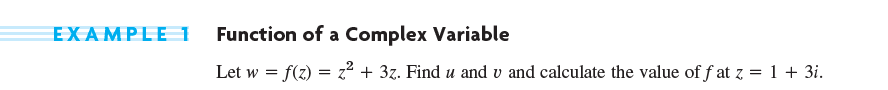
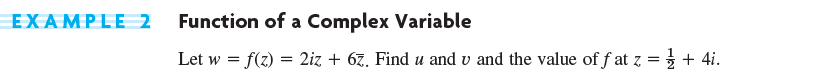
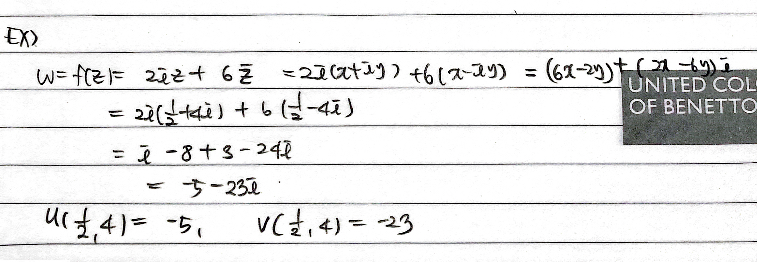
Limit, Continuity

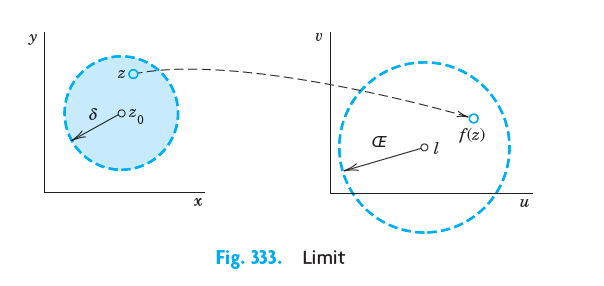
f(z)를 $z$에서 $z_0$로 향할 때 limit $l$을 가진다고 했을 때, 다음과 같이 표현 가능하다.

$${\displaystyle \underset{z\to z_0}{lim}f(z)=l}$$

여기서 f(z)는 $z_0$의 근방(neighborhood) 집합이다. $z_0$은 일종의 중심점이라고 생각하면 된다. 또한 f(z) 값은 $z$에서 $z_0$으로 갈 때(어느 방향이든 상관 없음) $l$에 가까이 되는 값을 가진다고 하면, $|z-z_0|<\delta$, \(z \neq z_0\) 를 만족하는 disk에 대해 다음 식을 만족하는 양의 실수 $ϵ$이 존재한다. 

$$|f(z)-l|<ϵ$$

 

continuity $z=z_0$일 때, 다음을 만족하면 된다.

$${\displaystyle \underset{z\to z_0}{lim}f(z)=f(z_0)}$$

 

 

circle과 disk의 차이

---

Derivative

$z_0$에서의 미분 계수는 다음과 같이 정의된다. 다음 식이 가능하다면 f(z) 는 $z_0$에서 미분가능하다.

$$\begin{gathered} f^{\prime }(z_0)={\displaystyle \underset{\mathrm{\Delta }z\to 0}{lim}\frac{f(z_0+\mathrm{\Delta }z)-f(z_0)}{\mathrm{\Delta }z}} \\ ={\displaystyle \underset{z\to z_0}{lim}\frac{f(z)-f(z_0)}{z-z_0}} \end{gathered}$$

미분과 관련된 성질은 우리가 흔히 고등학교 미적분에서 배운 것과 같다. 상수 계수는 미분 되지 않고, (f+g)' = f' + g', (fg)'=f'g+fg' 등의 성질을 만족한다. 

미분가능하지 않은 complex number에 관한 예시를 보겠다.

conjugate complex number는 미분 불가능하다!

---

Analytic Function(해석함수)

어떤 함수가 domain D에서 analytic 하다는 것은 그 domain 안의 점들이 그 domain에서 미분가능하다는 것이다. 다른 말로, $z_0$의 근방(neighborhood) 점들(domain D에 포함된다는 전제)에서 미분가능하다는 것이다.

 

+) 다항식에서 $f(z)=\frac{g(z)}{h(z)}$의 f(z)를 rational function이라고 한다.