티스토리 뷰
Engineering Mathematics
13.4 Cauchy-Riemann Equations. Laplace's Equation
hyuna_engineer 2023. 11. 20. 00:38
앞 장에서 \(w=f(z)=u(x,y) + iv(x,y) \)로 정의했었다. 만약, f가 domain D에서 analytic하다면 다음 조건들을 만족한다.
\[u_x = v_y, u_y = -v_z \]
이를 Cauchy-Riemann equations 라고 한다.
정리한 Theorem 은 다음 사진과 같다.

pf)



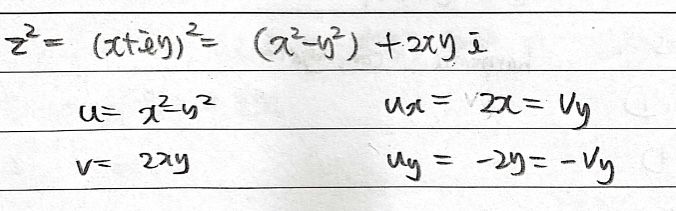
이 성질을 이용해서 해당 함수가 analytic한지 아닌지도 판단 가능하다.


이제 이를 Polar form으로 나타내면, \(z=r(cos\theta + i sin\theta)\), \(f(z) = u(r, \theta) + iv(r, \theta) \)이며 이를, Cauchy-Riemann equation에 대입하면, 다음과 같다.
\[u_r = \frac{1}{r} v_\theta , v_r = -\frac{1}{r} u_\theta \]
Laplace's Equation. Harmonic Functions


u, v 사이의 관계들을 harmonic function의 관계라고 한다.


'Engineering Mathematics' 카테고리의 다른 글
| 13.6 Trigonometric and Hyperbolic Functions. Euler's Formula (0) | 2023.11.23 |
|---|---|
| 13.5 Exponential Function (0) | 2023.11.23 |
| 13.3 Derivative. Analytic Function (0) | 2023.11.19 |
| 13.2 Polar Form of Complex Numbers. Powers and Roots (0) | 2023.11.19 |
| 13.1 Complex Numbers and Their Geometric Reprensentation (0) | 2023.11.19 |
