티스토리 뷰
13.7 Logarithm. General Power. Principal Value
hyuna_engineer 2023. 11. 23. 16:20
\[\ln z = w\]
위의 식처럼 복소수 w를 정의한다고 하자. 그러면 이에 대한 역은 다음과 같다.
\[e^{w} = z\]
w=u+iv라고 하고, polar form까지 적용하면,
\[e^{w} = e^{u+iv} = z= re^{i\theta} \cdots (1)\]
여기서, \(e^{u} = r, v=\theta\)임을 알 수 있다. (1)에서 양변에 ln을 취하면,
\[\ln z = \ln r + i \theta\]
\(\theta\)가 주기성을 갖지만, 이를 넣은 \(\theta\)는 결국 같은 각도를 나타내는데, ln z는 다른 값이 나오기에 Multi- valued하다. 여기서 하나의 branch만 가져와서 다음 식으로 나타내고자 한다.
\[Ln z = \ln \left| z \right| + i Arg z\]
다른 ln z를 혼동하지 않기 위해 Ln z로 표시한다. 이를 Principal value of ln z 라고 한다. 이렇게 하나의 값을 뽑아오는 multi-valued function을 single-valued로 만드는 "branch cut"이라고 한다.
- Multi-valued:
- Multi-valued는 여러 값이 가능한 것을 의미합니다. 복소수의 argument(위상)는 여러 개의 값으로 나타날 수 있습니다. 예를 들어, 특정 복소수 z에 대해 그 argument는 0에서 2π 사이의 값이 될 수 있습니다. 따라서 복소수의 argument는 다양한 값들을 갖게 되며, 이를 multi-valued라고 합니다.
- Single-valued:
- Single-valued는 한 가지 값만 가질 수 있는 것을 의미합니다. 함수가 single-valued일 때는 함수에 대한 입력값(도메인)에 대해 정확히 한 개의 출력값(레인지)만 가집니다. 복소수의 argument가 multi-valued이지만, 이를 single-valued로 만들기 위해 일반적으로 특정 branch를 선택하거나 principal value를 정의하여 특정 범위에서만 값을 가지도록 합니다.
여기서 위의 두 식을 혼합하면, 다음과 같이 나타낸다. (중요한 공식!!!)
\[\ln z = Ln z \pm 2n\pi i\]
z가 양의 실수이면, 즉, 허수 부분이 0이고, 각도 또한 0이므로 Arg z = 0이다. 즉 \(Ln z= \ln \left| z \right| + \pi i\)이다.
z가 음의 실수이면, Arg z = \(\pi\)이다. 즉, \(Ln z = \ln \left| z \right| + \pi i\)이다.
Logarithm이 Analytic할 때는 다음과 같다.

우리가 고등학교 미적분 수업에서 배운 것과 같은 내용이다. 하지만 이제는 증명을 해볼 수 있다.
pf)

General Powers
z를 밑으로 complex number c를 지수로 갖는 \[z^{c} = e^{c\ln z}\]에 대해 이 지수는 multi-valued이므로 여기서 13.5에 나온 것처럼 branch cut을 통해 single-valued를 구할 수 있다.
\[z^{c} = e^{c Ln z}\]
만약 \(c= \frac{1}{n}\)라고 하면,
\[z^c = \sqrt[n]{z} = e^{(1/n) \ln z}\]
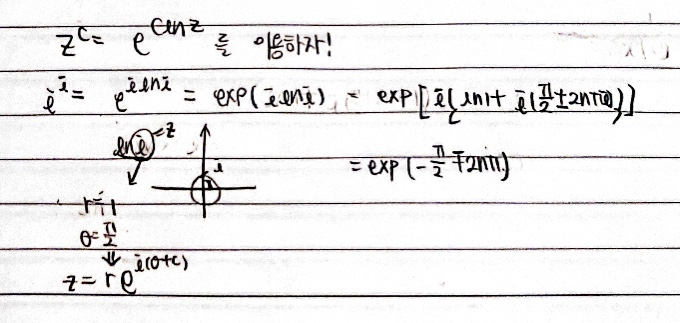
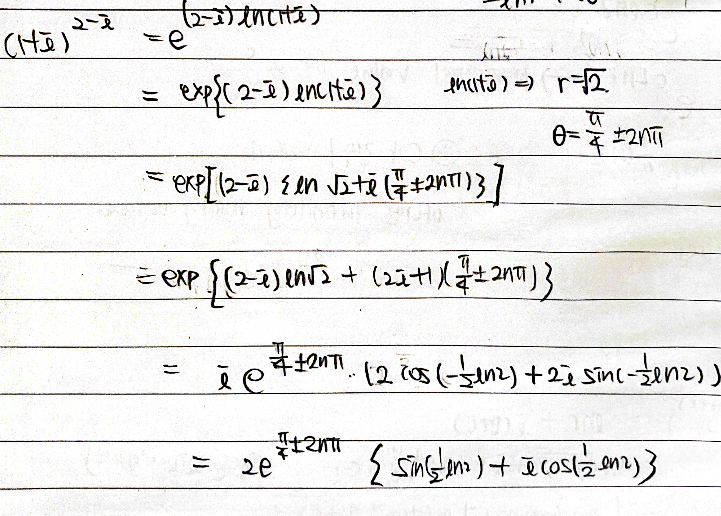
'Engineering Mathematics' 카테고리의 다른 글
| 14.2 Cauchy's Integral Theorem (0) | 2023.11.24 |
|---|---|
| 14.1 Line Integral in the Complex Plane (0) | 2023.11.24 |
| 13.6 Trigonometric and Hyperbolic Functions. Euler's Formula (0) | 2023.11.23 |
| 13.5 Exponential Function (0) | 2023.11.23 |
| 13.4 Cauchy-Riemann Equations. Laplace's Equation (0) | 2023.11.20 |
