티스토리 뷰
이번 장에서는 13장에서 배운 것을 토대로 평면으로 확장할 것이다.
우선 평면에서의 integral 전의 Line integral에 대해 알아보자. Complex definite integral(유한한 복소평면에서의 적분)을 Line integral, path integral이라고 하며, 다음 식과 같다.
\[\int_{c} f(z) dz\]
f(z)는 Complex plane의 curve path이다. Complex plane에 대한 따로 언급이 없는 한 smooth curve, 즉, 연속적이고 평면 접에서의 미분값 중에 0인 값은 없다고 하자. 또한 참고로, C-plane에 대해 z(t) = x(t) + iy(t)로 표현된다.

z(t)에 대해 미분을 진행하면 위와 같다.
Definition of the Complex Line Integral
Complex definite plane 위의 Line에서의 a에서 b까지들의 점들을 \(t_0=a\), \(t_1\) ...\(t_n=b\)라고 하자. 또한, \(\zeta_1\)을 \(z_0\)과 \(z_1\) 사이의 점이라고 해서, \(\zeta_n\)이 \(z_n-1\)과 \(z_n\) 사이의 점이라고 하자. 우선 이 점들에 대한 sum은 다음 식과 같다.
\[ S_n = \sum_{m=1}^{n} f(\zeta_m) \Delta z_m, \quad \text{where} \quad \Delta z_m = z_m - z_{m-1} \]
\]
\(S_n\)에 대한 limit를 취하면, line integral 위의 모든 점에서의 적분이 가능하며 이를 Line integral이라고 하는 것이다. 앞의 식처럼 도출되는 것이다.
\[\int_{c} f(z) dz \quad \text{or by} \quad \oint_c f(z) dz\]
Basic Properties Directly Implied by the Definition
1. Linearity (선형성)
\[\int_c [k_1f_1(z) + k_2f_2(z)] dz = k_1 \int_c f_1(z) dz + k_2 \int_c f_2(z) dz\]
2. Sense reverseal (-를 곱하면 적분 처음값과 끝값이 바뀜)
\[\int_{z_0}^{Z} f(z) dz = - \int_{Z}^{z_0} f(z) dz \]
3. Partitioning of path ( C가 c1과 c2의 line을 전부 포함한다는 전제)
\[\int_c f(z) dz = \int_{c_1} f(z) dz + \int_{c_2} f(z) dz \]
Existence of the Complex Line Integral
\(\zeta\) 또한 complex number이기에 \(zeta_m = \xi_m + i \eta_n\)라고 하고, \(\Delta z_m = \Delta x_m + i \Delta y_m\)라고 하자. 위의 summation을 다음과 같이 변환할 수 있다.
\[S_n = \sum \zeta_m \Delta z_m = \sum (u+iv)(\Delta x_m + i \Delta y_m \]
\[= \sum u \Delta x_m - \sum v \Delta y_m + i[\sum u \Delta y_m + \sum v \Delta x_m\]
참고로 \(u = u(\zeta_m, \eta_m), \quad v=v(\zeta_m, \eta_m)\) 이다.
여기에 limit를 취하면, 다음 식과 같이 정리된다.
\[\displaystyle \lim_{n \to \infty} S_n = \int_c f(z) dz\]
\[= \int_c udx - \int_c v dy +i [ \int_c u dy+ \int_c v dx]\]
Integration 구하는 첫 번째 방법 : Indefinite Integration and Substitution of Limits

증명은 14.2에서 진행한다. 일단은 우리가 흔히 아는 정적분처럼 계산한다고 생각하면 된다. simply connected 하며 Domain D에서 analytic한 f(z)에 대해서 진행한다. simply connected가 무엇인지 또한 다음 장에서 진행하니, 일단 단순히 하나의 disk라는 개념으로 이해하면 된다.
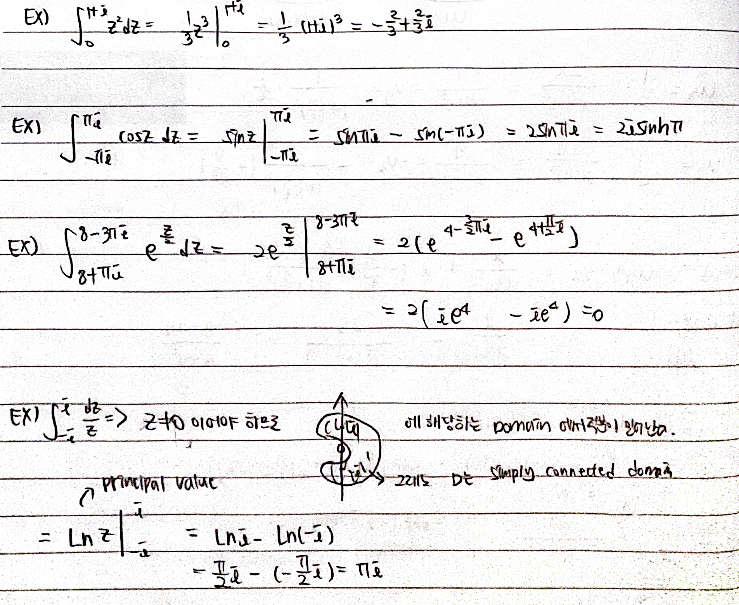
Integration 구하는 두 번째 방법 : Use of Representation of a Path

pf)

관련된 연습문제들을 보자.


Bounds for Integrals. ML-Inequality
Line Integral이 특정 값보다 항상 작다는 것을 나타내기 위함인데, 교재를 참고하자.

summation 진행한 것은 |f(z)| \(\neq\) M의 값과 curve의 length인 L의 값에 이하라는 것이다.

'Engineering Mathematics' 카테고리의 다른 글
| 14.3 -Cauchy's Integral Formula (0) | 2023.12.03 |
|---|---|
| 14.2 Cauchy's Integral Theorem (0) | 2023.11.24 |
| 13.7 Logarithm. General Power. Principal Value (0) | 2023.11.23 |
| 13.6 Trigonometric and Hyperbolic Functions. Euler's Formula (0) | 2023.11.23 |
| 13.5 Exponential Function (0) | 2023.11.23 |
